BayLum: An Introduction

Introduction

'BayLum' provides a collection of various R functions for Bayesian analysis of luminescence data. Amongst others, this includes data import, export, application of age models and palaeodose modelling.

Data can be processed simultaneously for various samples, including the input of multiple BIN/BINX-files per sample for single grain (SG) or multi-grain (MG) OSL measurements. Stratigraphic constraints and systematic errors can be added to constrain the analysis further.

For those who already know how to use R, 'BayLum' won’t be difficult to use, for all others, this brief introduction may be of help to make the first steps with R and the package 'BayLum' as convenient as possible.

Installing `BayLum’ package

If you read this document before having installed R itself, you should first visit the R project website and download and install R. You may also consider installing Rstudio, which provides an excellent desktop working environment for R; however it is not a prerequisite.

You will also need the external software JAGS (Just Another Gibs Sampler). Please visit the JAGS webpage and follow the installation instructions. Now you are nearly ready to work with ‘BayLum’.

If you have not yet installed ‘BayLum’, please run the following two R code lines to install ‘BayLum’ on your computer.

install.packages("BayLum", dependencies = TRUE)

Alternatively, you can load an already installed R package (here ‘BayLum’) into your session by using the following R call.

library(BayLum)

First steps: age analysis of one sample

Measurement data can be imported using two different options as detailed in the following:

Option 1: Using the conventional ‘BayLum’ folder structure (old)
Option 2: Using a single-setting config file (new)

Option 1: Import information from a BIN/BINX-file.

Let us consider the sample named samp1, which is the example dataset coming with the package. All information related to this sample is stored in a subfolder called also samp1. To test the package example, first, we add the path of the example dataset to the object path.

path <- paste0(system.file("extdata/", package = "BayLum"), "/")

Please note that for your own dataset (i.e. not included in the package) you have to replace this call by something like:

path <- "Users/Master_of_luminescence/Documents/MyFamousOSLData"

In our example the folder contains the following subfolders and files:

1	example.yml
2	FER1/bin.bin
3	FER1/Disc.csv
4	FER1/DoseEnv.csv
5	FER1/DoseSource.csv
6	FER1/rule.csv
7	samp1/bin.bin
8	samp1/DiscPos.csv
9	samp1/DoseEnv.csv
10	samp1/DoseSource.csv
11	samp1/rule.csv
12	samp2/bin.bin
13	samp2/DiscPos.csv
14	samp2/DoseEnv.csv
15	samp2/DoseSource.csv
16	samp2/rule.csv
17	yaml_config_reference.yml

See “What are the required files in each subfolder?” in the manual of Generate_DataFile() function for the meaning of these files.

To import your data, simply call the function Generate_DataFile():

DATA1 <-
  Generate_DataFile(
    Path = path,
    FolderNames = "samp1",
    Nb_sample = 1,
    verbose = FALSE)

Warning in Generate_DataFile(Path = path, FolderNames = "samp1", Nb_sample = 1, : 'Generate_DataFile' est obsolète.
Utilisez plutôt ‘create_DataFile()’.
Voir help("Deprecated")

Remarks

Data import/export

The import may take a while, in particular for large BIN/BINX-files. This can become annoying if you want to play with the data. In such situations, it makes sense to save your imported data somewhere else before continuing.

To save the obove imported data on your hardrive use

save(DATA1, file = "YourPath/DATA1.RData")

To load the data use

load(DATA1, file = "YourPath/DATA1.RData")

Data structure

To see the overall structure of the data generated from the BIN/BINX-file and the associated CSV-files, the following call can be used:

str(DATA1)

List of 9
 $ LT            :List of 1
  ..$ : num [1, 1:7] 2.042 0.842 1.678 3.826 4.258 ...
 $ sLT           :List of 1
  ..$ : num [1, 1:7] 0.344 0.162 0.328 0.803 0.941 ...
 $ ITimes        :List of 1
  ..$ : num [1, 1:6] 15 30 60 100 0 15
 $ dLab          : num [1:2, 1] 1.53e-01 5.89e-05
 $ ddot_env      : num [1:2, 1] 2.512 0.0563
 $ regDose       :List of 1
  ..$ : num [1, 1:6] 2.3 4.6 9.21 15.35 0 ...
 $ J             : num 1
 $ K             : num 6
 $ Nb_measurement: num 16

It reveals that DATA1 is basically a list with 9 elements:

Element	Content
`DATA1$LT`	$L_x$ / $T_x$ values from each sample
`DATA1$sLT`	$L_x$ / $T_x$ error values from each sample
`DATA1$ITimes`	Irradiation times
`DATA1$dLab`	The lab dose rate
`DATA1$ddot_env`	The environmental dose rate and its variance
`DATA1$regDose`	The regenerated dose points
`DATA1$J`	The number of aliquots selected for each BIN-file
`DATA1$K`	The number of regenerated dose points
`DATA1$Nb_measurement`	The number of measurements per BIN-file

Visualise Lx/Tx values and dose points

To get an impression on how your data look like, you can visualise them by using the function LT_RegenDose():

LT_RegenDose(
  DATA = DATA1,
  Path = path,
  FolderNames = "samp1",
  SampleNames = "samp1",
  Nb_sample = 1,
  nrow = NULL
)

Warning in LT_RegenDose(DATA = DATA1, Path = path, FolderNames = "samp1", : 'LT_RegenDose' est obsolète.
Utilisez plutôt ‘plot_RegDosePoints()’.
Voir help("Deprecated")

plot of chunk unnamed-chunk-10

Note that here we consider only one sample, and the name of the folder is the name of the sample. For that reason the argumetns were set to FolderNames = samp1 and SampleNames = samp1.

Generate data file from BIN/BINX-files of multi-grain OSL measurements

For a multi-grain OSL measurements, instead of Generate_DataFile(), the function Generate_DataFile_MG() should be used with similar parameters. The functions differ by their expectations: Disc.csv instead of DiscPos.csv file for Single-grain OSL Measurements. Please check type ?Generate_DataFile_MG for further information.

Option 2: Import data using `create_DataFile()`

With 'BayLum' >= v0.3.2 we introduced a new function called create_DataFile(), which will at some point in time replace the function Generate_DataFile() and Generate_DataFile_MG(). create_DataFile() works conceptionally very different from the approach detailed above. Key differences are:

The function uses a single configuration file for all samples and all measurement files
The very error prone subfolder structure is no longer needed
Measurement data can be imported with create_DataFile(), but also outside of the function and then passed on the functions. This enables the possibility of extensive pre-processing and selection of measurement data.

The configuration follows the so-called YAML format specification. For single sample the file looks as follows:

- sample: "samp1"
files: null
settings:
dose_source: { value: 0.1535, error: 0.00005891 }
dose_env: { value: 2.512, error: 0.05626 }
rules:
beginSignal: 6
endSignal: 8
beginBackground: 50
endBackground: 55
beginTest: 6
endTest: 8
beginTestBackground: 50
endTestBackground: 55
inflatePercent: 0.027
nbOfLastCycleToRemove: 1

In the case above, the configuration file assumes that data for samp1 are already imported and treated and a R object called samp1 is available in the global environment. The following example code reproduces this case:

## get example file path from package
yaml_file <- system.file("extdata/example.yml", package = "BayLum")
samp1_file <- system.file("extdata/samp1/bin.bin", package = "BayLum")

## read YAML manually and select only the first record 
config_file <- yaml::read_yaml(yaml_file)[[1]]

## import BIN/BINX files and select position 2 and grain 32 only
samp1 <- Luminescence::read_BIN2R(samp1_file, verbose = FALSE) |>
  subset(POSITION == 2 & GRAIN == 32)

## create the data file
DATA1 <- create_DataFile(config_file, verbose = FALSE)

Age computation

To compute the age of the sample samp1, you can run the following code:

Age <- Age_Computation(
  DATA = DATA1,
  SampleName = "samp1",
  PriorAge = c(10, 100),
  distribution = "cauchy",
  LIN_fit = TRUE,
  Origin_fit = FALSE,
  Iter = 10000
)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 6
   Unobserved stochastic nodes: 9
   Total graph size: 139

Initializing model

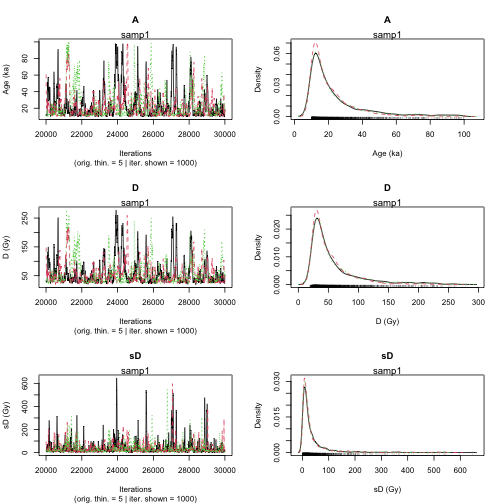
plot of chunk unnamed-chunk-12



>> Sample name <<
----------------------------------------------
samp1

>> Results of the Gelman and Rubin criterion of convergence <<
----------------------------------------------
     Point estimate Uppers confidence interval
A    1.043       1.102 
D    1.042       1.098 
sD   1.036       1.058 


---------------------------------------------------------------------------------------------------
 *** WARNING: The following information are only valid if the MCMC chains have converged  ***
---------------------------------------------------------------------------------------------------

parameter    Bayes estimate       Credible interval 
----------------------------------------------
A        25.061 
                         lower bound     upper bound
                 at level 95%    10          50.294 
                 at level 68%    10          21.841 
----------------------------------------------
D        62.212 
                         lower bound     upper bound
                 at level 95%    19.675          125.768 
                 at level 68%    22.385          55.487 
----------------------------------------------
sD       44.674 
                         lower bound     upper bound
                 at level 95%    0.15        126.445 
                 at level 68%    0.263       28.94

This also works if DATA1 is the output of Generate_DataFile_MG().

Remark 1: MCMC trajectories

If MCMC trajectories did not converge, you can add more iteration with the parameter Iter in the function Age_Computation(), for example Iter = 20000 or Iter = 50000. If it is not desirable to re-run the model from scratch, read the
To increase the precision of prior distribution, if not specified before you can use the argument PriorAge. For example: PriorAge= c(0.01,10) for a young sample and PriorAge = c(10,100) for an old sample.
If the trajectories are still not convergering, you should whether the choice you made with the argument distribution and dose-response curves are meaningful.

Remark 2: `LIN_fit` and `Origin_fit`, dose-response curves option

By default, a saturating exponential plus linear dose response curve is expected. However, you choose other formula by changing arguments LIN_fit and Origin_fit in the function.

Remark 3: `distribution`, equivalent dose dispersion option

By default, a cauchy distribution is assumed, but you can choose another distribution by replacing the word cauchy by gaussian, lognormal_A or lognormal_M for the argument distribution.

The difference between the models: lognormal_A and lognormal_M is that the equivalent dose dispersion are distributed according to:

a log-normal distribution with mean or average equal to the palaeodose for the first model
a log-normal distribution with median equal to the palaeodose for the second model.

Remark 4: `SavePdf` and `SaveEstimates` option

These two arguments allow to save the results to files.

SavePdf = TRUE create a PDF-file with MCMC trajectories of parameters A (age), D (palaeodose), sD (equivalent doses dispersion). You have to specify OutputFileName and OutputFilePath to define name and path of the PDF-file.
SaveEstimates = TRUE saves a CSV-file containing the Bayes estimates, the credible interval at 68% and 95% and the Gelman and Rudin test of convergence of the parameters A, D, sD. For the export the arguments OutputTableName and OutputTablePath have to be specified.

Remark 4: `PriorAge` option

By default, an age between 0.01 ka and 100 ka is expected. If the user has more informations on the sample, PriorAge should be modified accordingly.

For example, if you know that the sample is an older, you can set PriorAge=c(10,120). In contrast, if you know that the sample is younger, you may want to set PriorAge=c(0.001,10). Ages of $<=0$ are not possible. The minimum bound is 0.001.

Please note that the setting of PriorAge is not trivial, wrongly set boundaries are likely biasing your results.

Multiple BIN/BINX-files for one sample

In the previous example we considered only the simplest case: one sample, and one BIN/BINX-file. However, ‘BayLum’ allows to process multiple BIN/BINX-files for one sample. To work with multiple BIN/BINX-files, the names of the subfolders need to beset in argument Names and both files need to be located unter the same Path.

For the case

Names <- c("samp1", "samp2")

the call Generate_DataFile() (or Generate_DataFile_MG()) becomes as follows:

##argument setting
nbsample <- 1
nbbinfile <- length(Names)
Binpersample <- c(length(Names))

##call data file generator
DATA_BF <- Generate_DataFile(
  Path = path,
  FolderNames = Names,
  Nb_sample = nbsample,
  Nb_binfile = nbbinfile,
  BinPerSample = Binpersample,
  verbose = FALSE
)

Warning in Generate_DataFile(Path = path, FolderNames = Names, Nb_sample = nbsample, : 'Generate_DataFile' est obsolète.
Utilisez plutôt ‘create_DataFile()’.
Voir help("Deprecated")

##calculate the age
Age <- Age_Computation(
  DATA = DATA_BF,
  SampleName = Names,
  BinPerSample = Binpersample
)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 12
   Unobserved stochastic nodes: 15
   Total graph size: 221

Initializing model

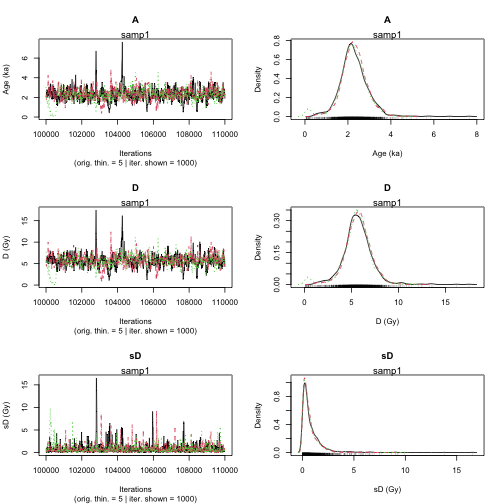
plot of chunk unnamed-chunk-14



>> Sample name <<
----------------------------------------------
samp1 samp2

>> Results of the Gelman and Rubin criterion of convergence <<
----------------------------------------------
     Point estimate Uppers confidence interval
A    1.018       1.023 
D    1.022       1.027 
sD   1.044       1.057 


---------------------------------------------------------------------------------------------------
 *** WARNING: The following information are only valid if the MCMC chains have converged  ***
---------------------------------------------------------------------------------------------------

parameter    Bayes estimate       Credible interval 
----------------------------------------------
A        2.312 
                         lower bound     upper bound
                 at level 95%    0.86        3.819 
                 at level 68%    1.65        2.728 
----------------------------------------------
D        5.75 
                         lower bound     upper bound
                 at level 95%    2.602       9.545 
                 at level 68%    4.453       6.886 
----------------------------------------------
sD       0.881 
                         lower bound     upper bound
                 at level 95%    0.003       3.318 
                 at level 68%    0.003       0.846

Age analysis of various samples

Generate data file from BIN/BINX-files

The function Generate_DataFile() (or Generate_DataFile_MF()) can process multiple files simultaneously including multiple BIN/BINX-files per sample.

We assume that we are interested in two samples named: sample1 and sample2. In addition, we have two BIN/BINX-files for the first sample named: sample1-1 and sample1-2, and one BIN-file for the 2nd sample named sample2-1. In such case, we need three subfolders named sample1-1, sample1-2 and sample2-1; which each subfolder containing only one BIN-file named bin.bin, and its associated files DiscPos.csv, DoseEnv.csv, DoseSourve.csv and rule.csv. All of these 3 subfolders must be located in path.

To fill the argument corectly BinPerSample: $binpersample=c(\underbrace{2}_{\text{sample 1: 2 bin files}},\underbrace{1}_{\text{sample 2: 1 bin file}})$

Names <-
  c("sample1-1", "sample1-2", "sample2-1") # give the name of the folder datat
nbsample <- 2    # give the number of samples
nbbinfile <- 3   # give the number of bin files
DATA <- Generate_DataFile(
  Path = path,
  FolderNames = Names,
  Nb_sample = nbsample,
  Nb_binfile = nbbinfile,
  BinPerSample = binpersample
)

Combine files using the function `combine_DataFiles()`

If the user has already saved informations imported with Generate_DataFile() function (or Generate_DataFile_MG() function) these data can be concatenate with the function combine_DataFiles().

For example, if DATA1 is the output of sample named “GDB3”, and DATA2 is the output of sample “GDB5”, both data can be merged with the following call:

data("DATA1", envir = environment())
data("DATA2", envir = environment())
DATA3 <- combine_DataFiles(L1 = DATA2, L2 = DATA1)
str(DATA3)

List of 11
 $ LT            :List of 2
  ..$ : num [1:188, 1:6] 4.54 2.73 2.54 2.27 1.48 ...
  ..$ : num [1:101, 1:6] 5.66 6.9 4.05 3.43 4.97 ...
 $ sLT           :List of 2
  ..$ : num [1:188, 1:6] 0.333 0.386 0.128 0.171 0.145 ...
  ..$ : num [1:101, 1:6] 0.373 0.315 0.245 0.181 0.246 ...
 $ ITimes        :List of 2
  ..$ : num [1:188, 1:5] 40 40 40 40 40 40 40 40 40 40 ...
  ..$ : num [1:101, 1:5] 160 160 160 160 160 160 160 160 160 160 ...
 $ dLab          : num [1:2, 1:2] 1.53e-01 5.89e-05 1.53e-01 5.89e-05
 $ ddot_env      : num [1:2, 1:2] 2.512 0.0563 2.26 0.0617
 $ regDose       :List of 2
  ..$ : num [1:188, 1:5] 6.14 6.14 6.14 6.14 6.14 6.14 6.14 6.14 6.14 6.14 ...
  ..$ : num [1:101, 1:5] 24.6 24.6 24.6 24.6 24.6 ...
 $ J             : num [1:2] 188 101
 $ K             : num [1:2] 5 5
 $ Nb_measurement: num [1:2] 14 14
 $ SampleNames   : chr [1:2] "samp 1" "samp 1"
 $ Nb_sample     : num 2
 - attr(*, "originator")= chr "create_DataFile"

The data structure should become as follows

2 lists (1 list per sample) for DATA$LT, DATA$sLT, DATA1$ITimes and DATA1$regDose
A matrix with 2 columns (1 line per sample) for DATA1$dLab, DATA1$ddot_env
2 integers (1 integer per BIN files here we have 1 BIN-file per sample) for DATA1$J, DATA1$K, DATA1$Nb_measurement.

Single-grain and multiple-grain OSL measurements can be merged in the same way. To plot the $L/T$ as a function of the regenerative dose the function LT_RegenDose() can be used again:

plot_RegDosePoints(DATA3)

Note: In the example DATA3 contains information from the samples ‘GDB3’ and ‘GDB5’, which are single-grain OSL measurements. For a correct treatment the argument SG has to be manually set by the user. Please see the function manual for further details.

Age analysis without stratigraphic constraints

If no stratigraphic constraints were set, the following code can be used to analyse the age of the sample GDB5 and GDB3 simultaneously.

priorage = c(1, 10, 10, 100)
Age <- AgeS_Computation(
  DATA = DATA3,
  Nb_sample = 2,
  SampleNames = c("GDB5", "GDB3"),
  PriorAge = priorage,
  distribution = "cauchy",
  LIN_fit = TRUE,
  Origin_fit = FALSE,
  Iter = 1000, 
  jags_method = "rjags"
)

Warning: No initial values were provided - JAGS will use the same initial values for all chains

Compiling rjags model...
Calling the simulation using the rjags method...
Adapting the model for 1000 iterations...
Running the model for 5000 iterations...
Simulation complete
Calculating summary statistics...
Calculating the Gelman-Rubin statistic for 6 variables....
Finished running the simulation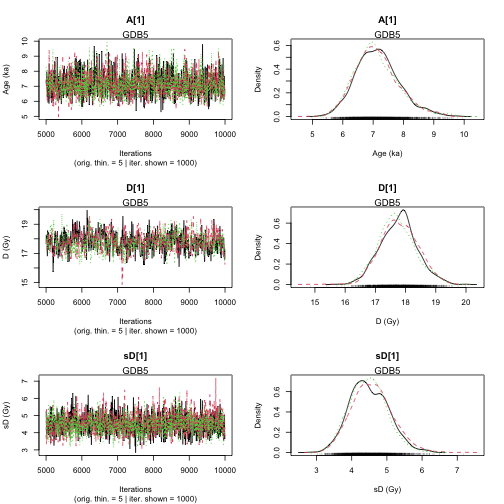

plot of chunk unnamed-chunk-18



>> Results of the Gelman and Rubin criterion of convergence <<
----------------------------------------------
 Sample name:  GDB5 
---------------------
         Point estimate Uppers confidence interval
A_GDB5   1.002       1.005 
D_GDB5   1.003       1.012 
sD_GDB5      1.006       1.021 
----------------------------------------------
 Sample name:  GDB3 
---------------------
         Point estimate Uppers confidence interval
A_GDB3   1       1 
D_GDB3   1.001       1.002 
sD_GDB3      1.001       1.005 


---------------------------------------------------------------------------------------------------
 *** WARNING: The following information are only valid if the MCMC chains have converged  ***
---------------------------------------------------------------------------------------------------



>> Bayes estimates of Age, Palaeodose and its dispersion for each sample and credible interval <<
----------------------------------------------
 Sample name:  GDB5 
---------------------
Parameter    Bayes estimate       Credible interval 
 A_GDB5      7.132 
                         lower bound     upper bound
                 at level 95%    5.783       8.596 
                 at level 68%    6.298       7.677 

Parameter    Bayes estimate       Credible interval 
 D_GDB5      17.798 
                         lower bound     upper bound
                 at level 95%    16.725          19.004 
                 at level 68%    17.145          18.332 

Parameter    Bayes estimate       Credible interval 
sD_GDB5      4.53 
                         lower bound     upper bound
                 at level 95%    3.544       5.782 
                 at level 68%    4.028       5.142 
----------------------------------------------
 Sample name:  GDB3 
---------------------
Parameter    Bayes estimate       Credible interval 
 A_GDB3      46.979 
                         lower bound     upper bound
                 at level 95%    36.343          57.758 
                 at level 68%    40.774          51.082 

Parameter    Bayes estimate       Credible interval 
 D_GDB3      104.689 
                         lower bound     upper bound
                 at level 95%    96.694          112.104 
                 at level 68%    101.184         108.653 

Parameter    Bayes estimate       Credible interval 
sD_GDB3      16.236 
                         lower bound     upper bound
                 at level 95%    9.985       21.678 
                 at level 68%    12.11       18.146 

----------------------------------------------

plot of chunk unnamed-chunk-18

Note: For an automated parallel processing you can set the argument jags_method = "rjags" to jags_method = "rjparallel".

Remarks

As for the function Age_computation(), the age for each sample is set by default between 0.01 ka and 100 ka. If you have more informations on your samples it is possible to change PriorAge parameters. PriorAge is a vector of size = 2*$Nb_sample, the two first values of PriorAge concern the 1st sample, the next two values the 2nd sample and so on.

For example, if you know that sample named GDB5 is a young sample whose its age is between 0.01 ka and 10 ka, and GDB3 is an old sample whose age is between 10 ka and 100 ka, $PriorAge=c(\underbrace{0.01,10}_{GDB5\ prior\ age},\underbrace{10,100}_{GDB3\ prior\ age})$

Age analysis with stratigraphic constraints

With the function AgeS_Computation() it is possible to take the stratigraphic relations between samples into account and define constraints.

For example, we know that GDB5 is in a higher stratigraphical position, hence it likely has a younger age than sample GDB3.

Ordering samples

To take into account stratigraphic constraints, the information on the samples need to be ordered. Either you enter a sample name (corresponding to subfolder names) in Names parameter of the function Generate_DataFile(), ordered by order of increasing ages or you enter saved .RData informations of each sample in combine_DataFiles(), ordered by increasing ages.

# using Generate_DataFile function
Names <- c("samp1", "samp2")
nbsample <- 2
DATA3 <- Generate_DataFile(
  Path = path,
  FolderNames = Names,
  Nb_sample = nbsample,
  verbose = FALSE
)

Warning in Generate_DataFile(Path = path, FolderNames = Names, Nb_sample = nbsample, : 'Generate_DataFile' est obsolète.
Utilisez plutôt ‘create_DataFile()’.
Voir help("Deprecated")

# using the function combine_DataFiles()
data(DATA1, envir = environment()) # .RData on sample GDB3
data(DATA2, envir = environment()) # .RData on sample GDB5
DATA3 <- combine_DataFiles(L1 = DATA1, L2 = DATA2)

Define matrix to set stratigraphic constraints

Let SC be the matrix containing all information on stratigraphic relations for this two samples. This matrix is defined as follows:

matrix dimensions: the row number of StratiConstraints matrix is equal to Nb_sample+1, and column number is equal to $Nb\_sample$ .
first matrix row: for all $i$ in $\{1,...,Nb\_Sample\}$ , StratiConstraints[1,i] <- 1, means that the lower bound of the sample age given in PriorAge[2i-1] for the sample whose number ID is equal to $i$ is taken into account
sample relations: for all $j$ in ${2,…,Nb_Sample+1}$ and all $i$ in $\{j,...,Nb\_Sample\}$ , StratiConstraints[j,i] <- 1 if the sample age whose ID is equal to $j-1$ is lower than the sample age whose ID is equal to $i$ . Otherwise, StratiConstraints[j,i] <- 0.

To the define such matrix the function SCMatrix() can be used:

SC <- SCMatrix(Nb_sample = 2,
               SampleNames = c("samp1", "samp2"))

In our case: 2 samples, SC is a matrix with 3 rows and 2 columns. The first row contains c(1,1) (because we take into account the prior ages), the second line contains c(0,1) (sample 2, named samp2 is supposed to be older than sample 1, named samp1) and the third line contains c(0,0) (sample 2, named samp2 is not younger than the sample 1, here named samp1). We can also fill the matrix with the stratigraphic relations as follow:

SC <- matrix(
  data = c(1, 1, 0, 1, 0, 0),
  ncol = 2,
  nrow = (2 + 1),
  byrow = T
)

Age computation

Age <-
  AgeS_Computation(
    DATA = DATA3,
    Nb_sample = 2,
    SampleNames = c("samp1", "samp2"),
    PriorAge = priorage,
    distribution = "cauchy",
    LIN_fit = TRUE,
    Origin_fit = FALSE,
    StratiConstraints = SC,
    Iter = 1000, 
    jags_method = 'rjags')

Warning: No initial values were provided - JAGS will use the same initial values for all chains

Compiling rjags model...
Calling the simulation using the rjags method...
Adapting the model for 1000 iterations...
Running the model for 5000 iterations...
Simulation complete
Calculating summary statistics...
Calculating the Gelman-Rubin statistic for 6 variables....
Finished running the simulation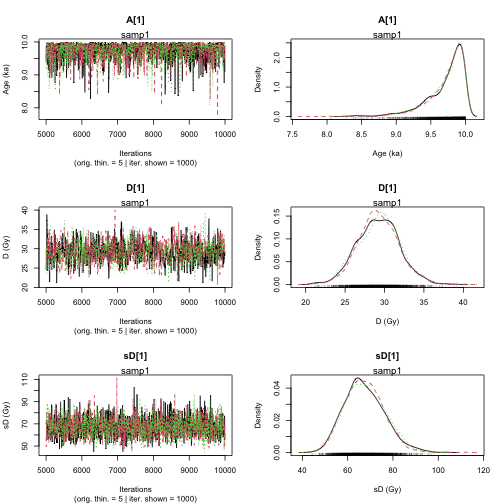

plot of chunk unnamed-chunk-23



>> Results of the Gelman and Rubin criterion of convergence <<
----------------------------------------------
 Sample name:  samp1 
---------------------
         Point estimate Uppers confidence interval
A_samp1      1.003       1.005 
D_samp1      1       1.002 
sD_samp1     1.003       1.009 
----------------------------------------------
 Sample name:  samp2 
---------------------
         Point estimate Uppers confidence interval
A_samp2      1.004       1.008 
D_samp2      1.005       1.017 
sD_samp2     1.002       1.01 


---------------------------------------------------------------------------------------------------
 *** WARNING: The following information are only valid if the MCMC chains have converged  ***
---------------------------------------------------------------------------------------------------



>> Bayes estimates of Age, Palaeodose and its dispersion for each sample and credible interval <<
----------------------------------------------
 Sample name:  samp1 
---------------------
Parameter    Bayes estimate       Credible interval 
 A_samp1     9.711 
                         lower bound     upper bound
                 at level 95%    9.126       10 
                 at level 68%    9.677       10 

Parameter    Bayes estimate       Credible interval 
 D_samp1     29.26 
                         lower bound     upper bound
                 at level 95%    23.914          34.493 
                 at level 68%    26.756          32.052 

Parameter    Bayes estimate       Credible interval 
sD_samp1     67.869 
                         lower bound     upper bound
                 at level 95%    51.164          84.839 
                 at level 68%    57.714          74.182 
----------------------------------------------
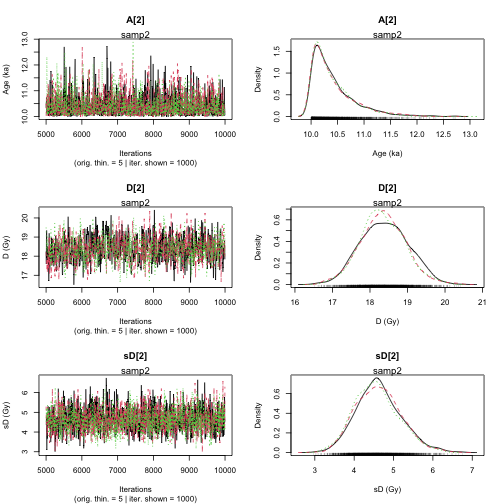
 Sample name:  samp2 
---------------------
Parameter    Bayes estimate       Credible interval 
 A_samp2     10.413 
                         lower bound     upper bound
                 at level 95%    10          11.236 
                 at level 68%    10          10.469 

Parameter    Bayes estimate       Credible interval 
 D_samp2     18.343 
                         lower bound     upper bound
                 at level 95%    17.089          19.48 
                 at level 68%    17.62       18.846 

Parameter    Bayes estimate       Credible interval 
sD_samp2     4.619 
                         lower bound     upper bound
                 at level 95%    3.588       5.669 
                 at level 68%    4.003       5.09 

----------------------------------------------

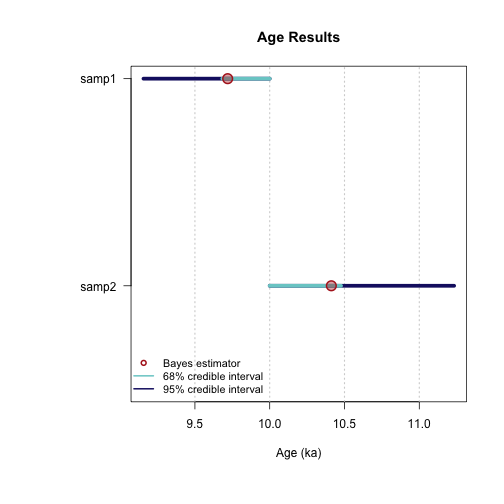
plot of chunk unnamed-chunk-23

Thee results can be also be used for an alternative graphical representation:

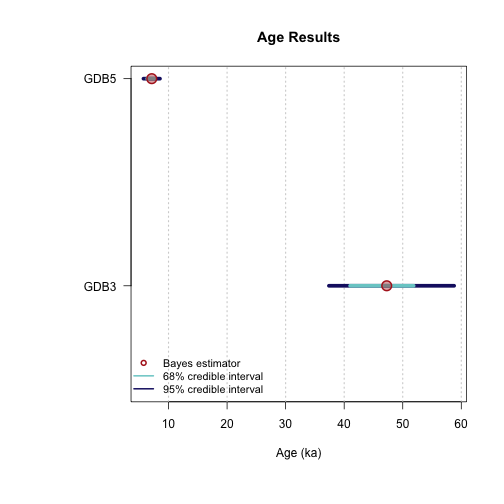
plot_Ages(Age, plot_mode = "density")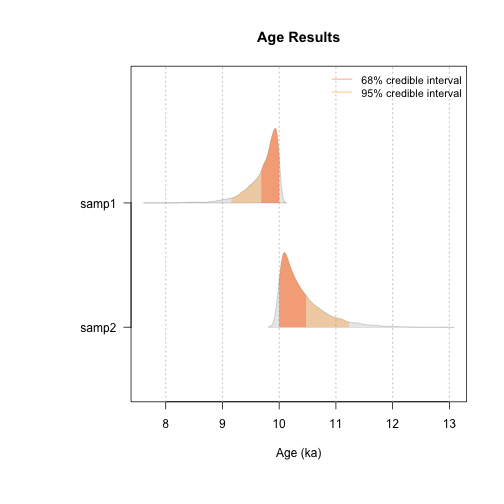

plot of chunk unnamed-chunk-24

  SAMPLE    AGE HPD68.MIN HPD68.MAX HPD95.MIN HPD95.MAX ALT_SAMPLE_NAME AT
1  samp1  9.711     9.677    10.000     9.126    10.000              NA  2
2  samp2 10.413    10.000    10.469    10.000    11.236              NA  1

When MCMC trajectories did not converge

If MCMC trajectories did not converge, it means we should run additional MCMC iterations.
For AgeS_computation() and Age_OSLC14() models we can run additional iterations by supplying the function output back into the parent function. In the following, notice we are using the output of the previous AgeS_computation() example, namely Age. The key argument to set/change is DATA.

Age <- AgeS_Computation(
  DATA = Age,
  Nb_sample = 2,
  SampleNames = c("GDB5", "GDB3"),
  PriorAge = priorage,
  distribution = "cauchy",
  LIN_fit = TRUE,
  Origin_fit = FALSE,
  Iter = 1000, 
  jags_method = "rjags"
)

Calling the simulation using the rjags method...
Note: the model did not require adaptation
Burning in the model for 4000 iterations...
Running the model for 5000 iterations...
Simulation complete
Calculating summary statistics...
Calculating the Gelman-Rubin statistic for 6 variables....
Finished running the simulation

plot of chunk unnamed-chunk-25



>> Results of the Gelman and Rubin criterion of convergence <<
----------------------------------------------
 Sample name:  GDB5 
---------------------
         Point estimate Uppers confidence interval
A_GDB5   1       1 
D_GDB5   1.001       1.004 
sD_GDB5      1.001       1.005 
----------------------------------------------
 Sample name:  GDB3 
---------------------
         Point estimate Uppers confidence interval
A_GDB3   1.008       1.012 
D_GDB3   1.009       1.031 
sD_GDB3      1.007       1.026 


---------------------------------------------------------------------------------------------------
 *** WARNING: The following information are only valid if the MCMC chains have converged  ***
---------------------------------------------------------------------------------------------------



>> Bayes estimates of Age, Palaeodose and its dispersion for each sample and credible interval <<
----------------------------------------------
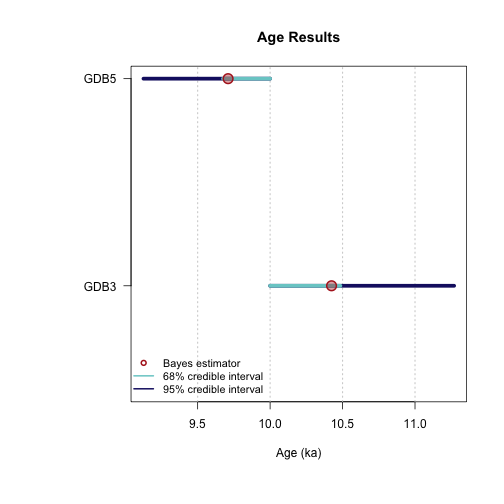
 Sample name:  GDB5 
---------------------
Parameter    Bayes estimate       Credible interval 
 A_GDB5      9.724 
                         lower bound     upper bound
                 at level 95%    9.154       10 
                 at level 68%    9.687       10 

Parameter    Bayes estimate       Credible interval 
 D_GDB5      29.372 
                         lower bound     upper bound
                 at level 95%    23.658          34.505 
                 at level 68%    26.635          32.055 

Parameter    Bayes estimate       Credible interval 
sD_GDB5      67.561 
                         lower bound     upper bound
                 at level 95%    50.632          84.409 
                 at level 68%    59.654          76.278 
----------------------------------------------
 Sample name:  GDB3 
---------------------
Parameter    Bayes estimate       Credible interval 
 A_GDB3      10.406 
                         lower bound     upper bound
                 at level 95%    10          11.176 
                 at level 68%    10          10.468 

Parameter    Bayes estimate       Credible interval 
 D_GDB3      18.29 
                         lower bound     upper bound
                 at level 95%    17.184          19.532 
                 at level 68%    17.675          18.837 

Parameter    Bayes estimate       Credible interval 
sD_GDB3      4.557 
                         lower bound     upper bound
                 at level 95%    3.526       5.591 
                 at level 68%    3.975       5.059 

----------------------------------------------

plot of chunk unnamed-chunk-25

References

Combès, B., Philippe, A., Lanos, P., Mercier, N., Tribolo, C., Guerin, G., Guibert, P., Lahaye, C., 2015. A Bayesian central equivalent dose model for optically stimulated luminescence dating. Quaternary Geochronology 28, 62-70. doi: 10.1016/j.quageo.2015.04.001

Combès, B., Philippe, A., 2017. Bayesian analysis of individual and systematic multiplicative errors for estimating ages with stratigraphic constraints in optically stimulated luminescence dating. Quaternary Geochronology 39, 24–34. doi: 10.1016/j.quageo.2017.02.003

Philippe, A., Guérin, G., Kreutzer, S., 2019. BayLum - An R package for Bayesian analysis of OSL ages: An introduction. Quaternary Geochronology 49, 16-24. doi: 10.1016/j.quageo.2018.05.009

Claire Christophe, Anne Philippe, Sebastian Kreutzer, Guillaume Guérin, Frederik Baumgarten

Updated for BayLum package version 0.3.2 (2024-09-18)

Introduction

Installing `BayLum’ package

First steps: age analysis of one sample

Option 1: Import information from a BIN/BINX-file.

Remarks

Data import/export

Data structure

Visualise Lx/Tx values and dose points

Generate data file from BIN/BINX-files of multi-grain OSL measurements

Option 2: Import data using `create_DataFile()`

Age computation

Remark 1: MCMC trajectories

Remark 2: `LIN_fit` and `Origin_fit`, dose-response curves option

Remark 3: `distribution`, equivalent dose dispersion option

Remark 4: `SavePdf` and `SaveEstimates` option

Remark 4: `PriorAge` option

Multiple BIN/BINX-files for one sample

Age analysis of various samples

Generate data file from BIN/BINX-files

Combine files using the function `combine_DataFiles()`

Age analysis without stratigraphic constraints

Remarks

Age analysis with stratigraphic constraints

Ordering samples

Define matrix to set stratigraphic constraints

Age computation

When MCMC trajectories did not converge

References

Further reading

For more details on the diagnostic of Markov chains

For details on the here used dataset

BayLum: An Introduction

Claire Christophe, Anne Philippe, Sebastian Kreutzer, Guillaume Guérin, Frederik Baumgarten

Updated for BayLum package version 0.3.2 (2024-09-18)

Introduction

Installing `BayLum’ package

First steps: age analysis of one sample

Option 1: Import information from a BIN/BINX-file.

Remarks

Data import/export

Data structure

Visualise Lx/Tx values and dose points

Generate data file from BIN/BINX-files of multi-grain OSL measurements

Option 2: Import data using create_DataFile()

Age computation

Remark 1: MCMC trajectories

Remark 2: LIN_fit and Origin_fit, dose-response curves option

Remark 3: distribution, equivalent dose dispersion option

Remark 4: SavePdf and SaveEstimates option

Remark 4: PriorAge option

Multiple BIN/BINX-files for one sample

Age analysis of various samples

Generate data file from BIN/BINX-files

Combine files using the function combine_DataFiles()

Age analysis without stratigraphic constraints

Remarks

Age analysis with stratigraphic constraints

Ordering samples

Define matrix to set stratigraphic constraints

Age computation

When MCMC trajectories did not converge

References

Further reading

For more details on the diagnostic of Markov chains

For details on the here used dataset

Option 2: Import data using `create_DataFile()`

Remark 2: `LIN_fit` and `Origin_fit`, dose-response curves option

Remark 3: `distribution`, equivalent dose dispersion option

Remark 4: `SavePdf` and `SaveEstimates` option

Remark 4: `PriorAge` option

Combine files using the function `combine_DataFiles()`