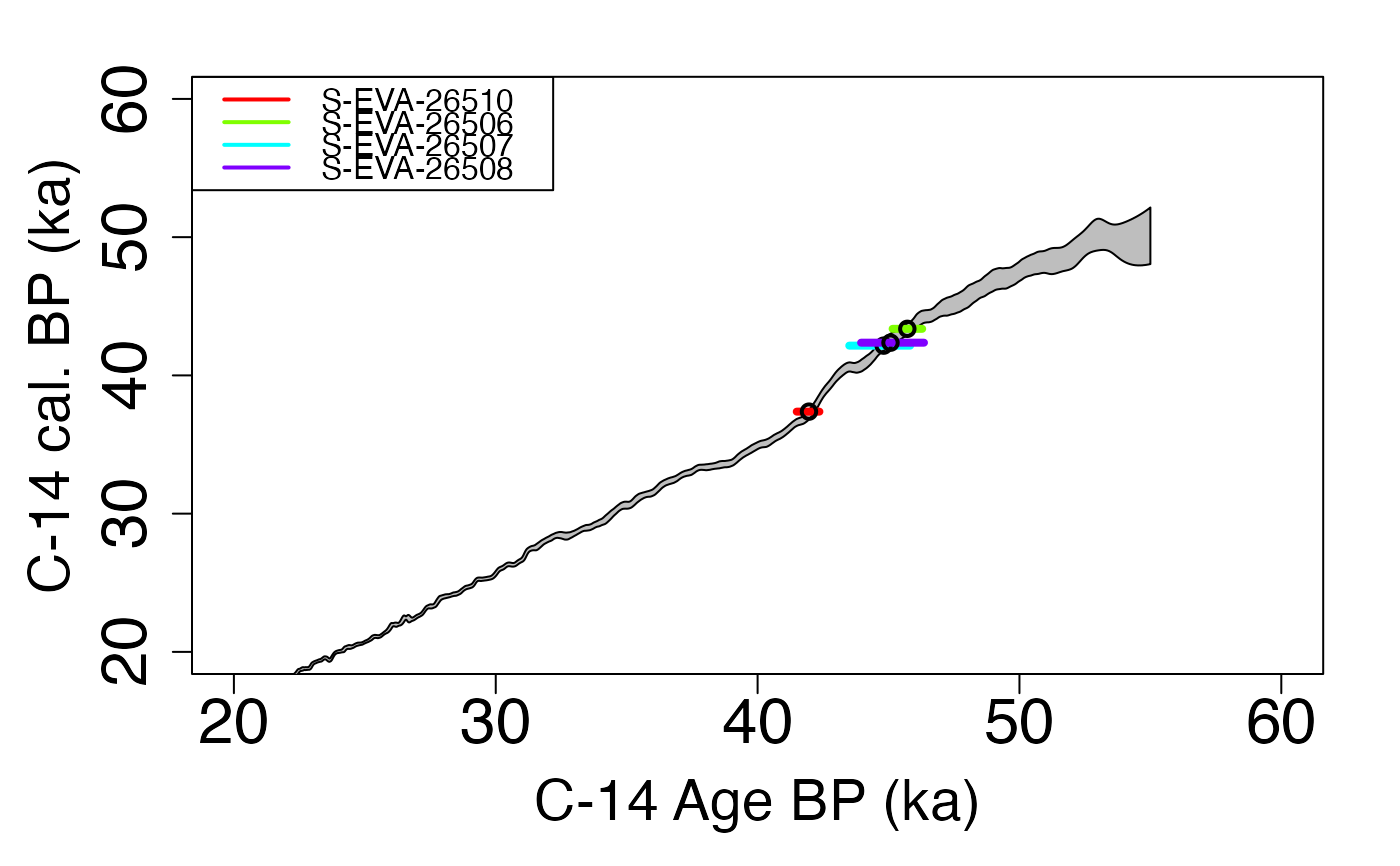
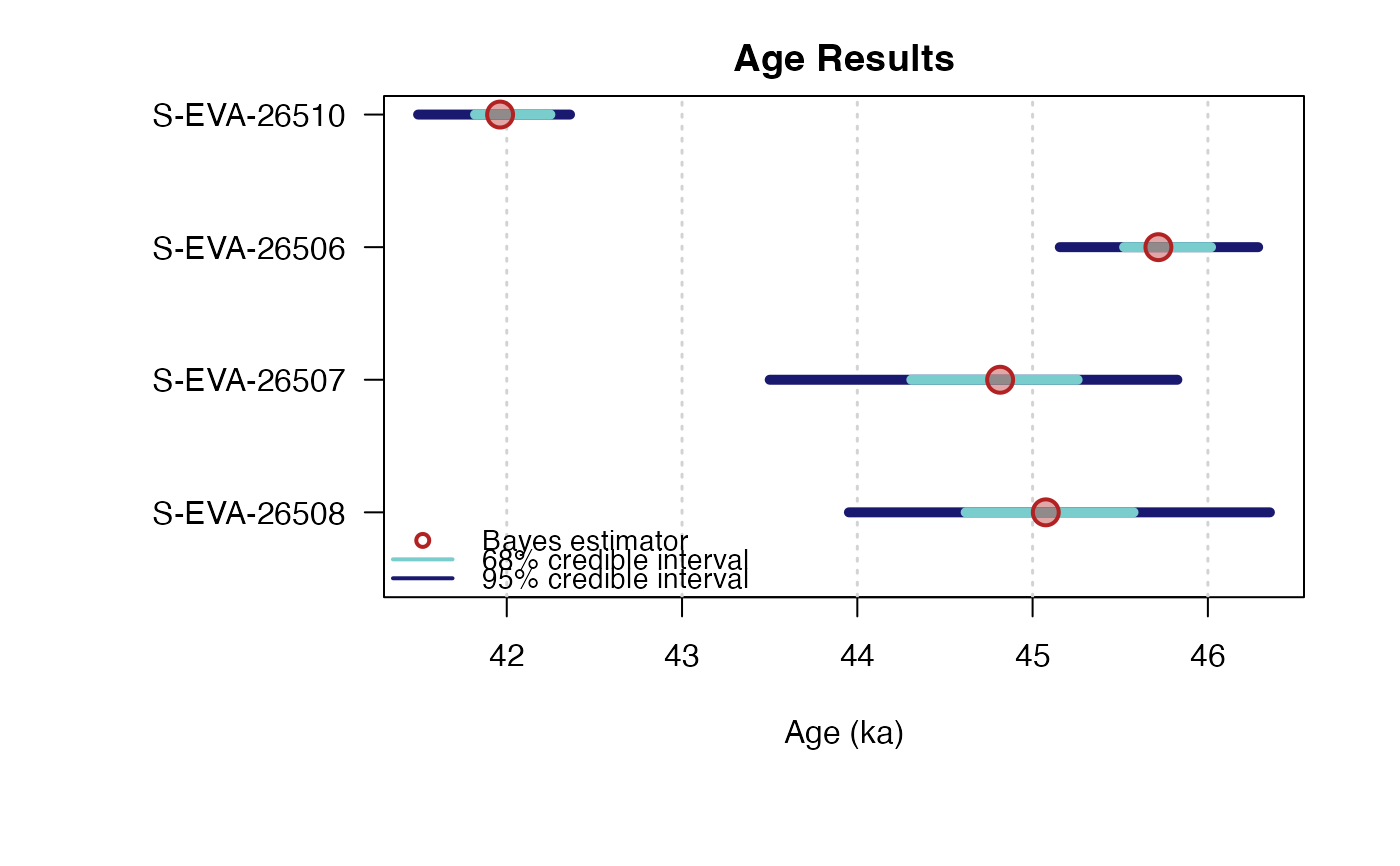
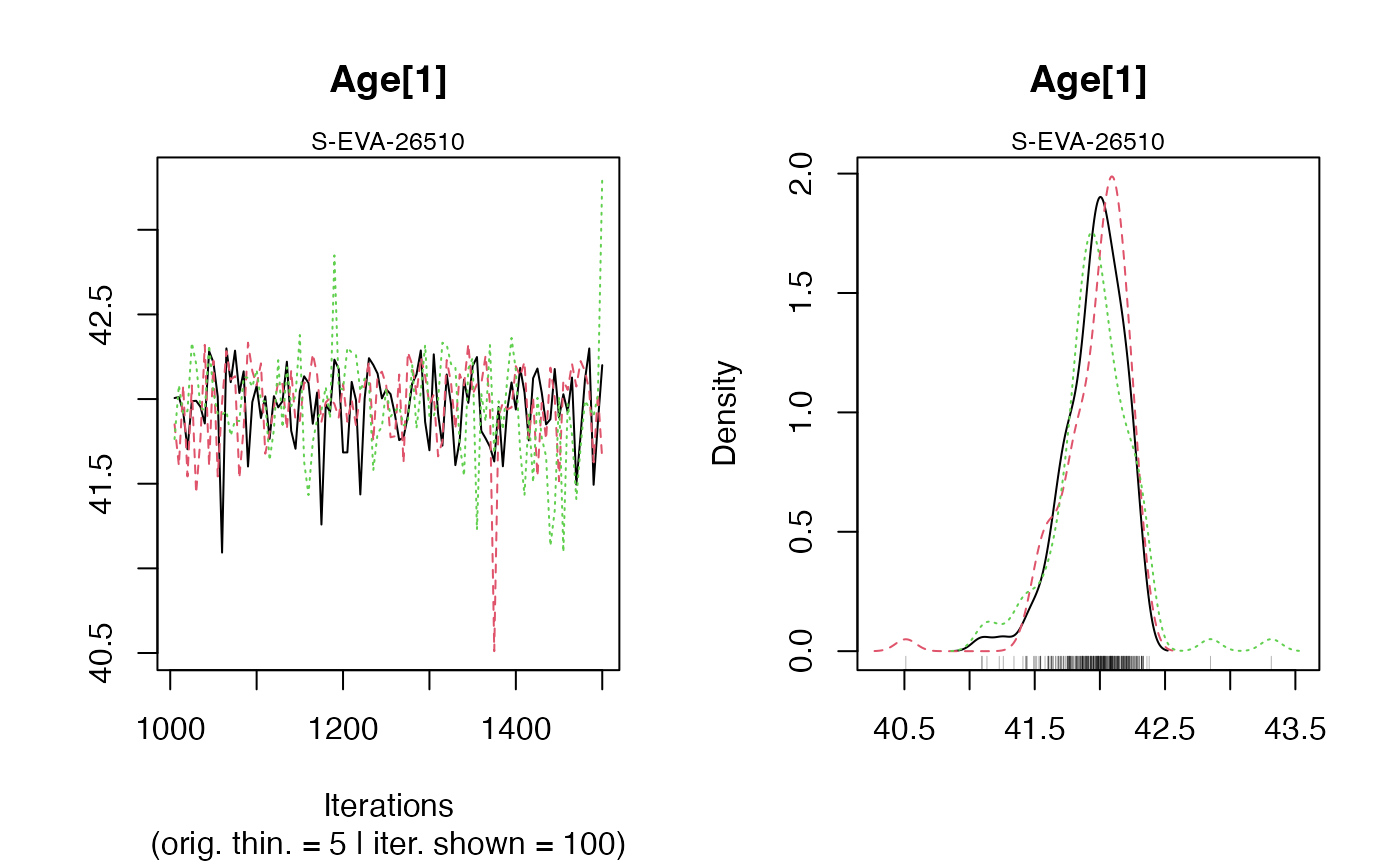
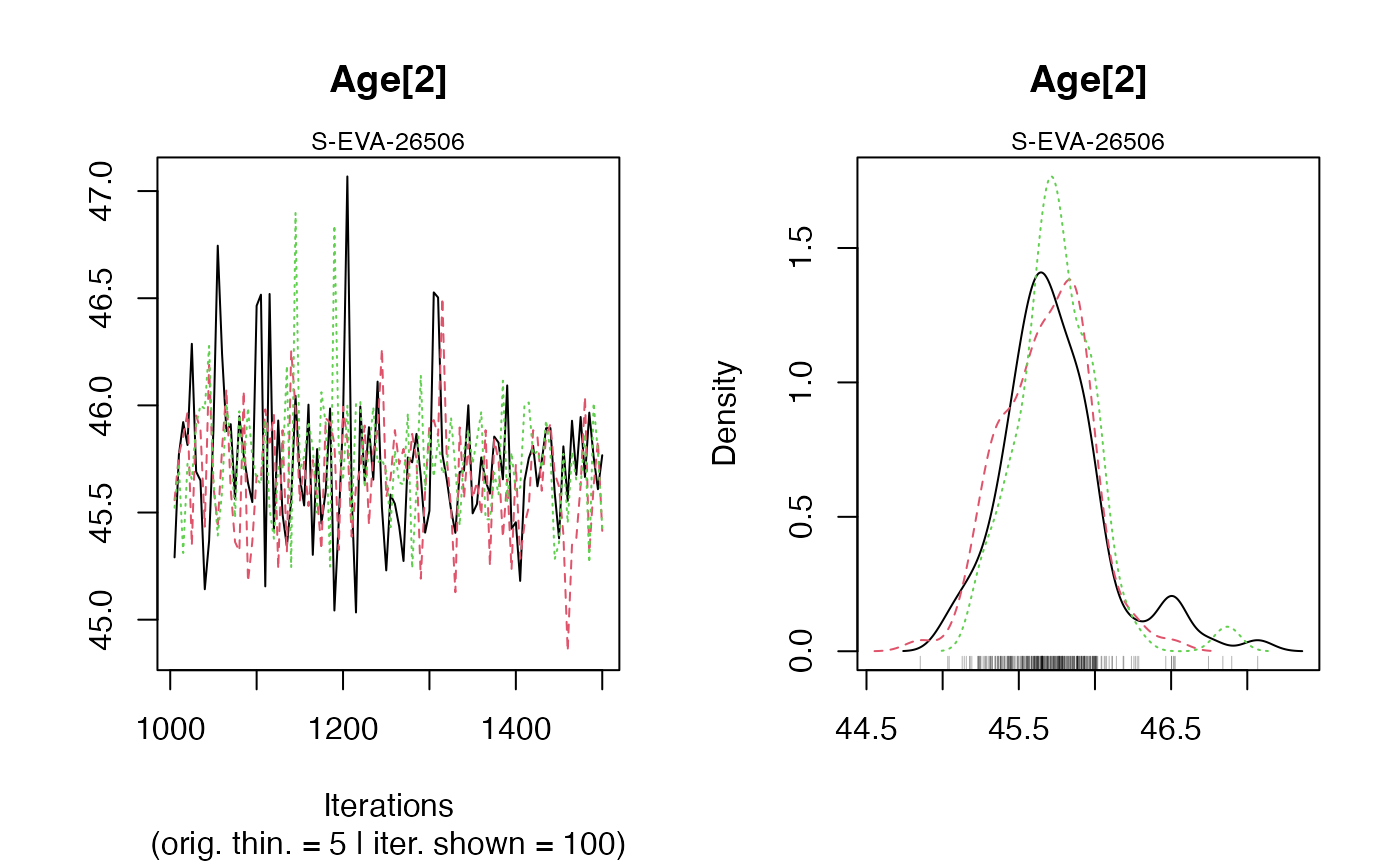
Bayesian analysis for C-14 age estimations of various samples

Source: R/AgeC14_Computation.R

This function calibrates the C-14 age of samples to get an age (in ka). The user can choose one of the following radiocarbon calibration curve: Northern or Southern Hemisphere or marine atmospheric. It must be the same curve for all samples.

AgeC14_Computation(
  Data_C14Cal,
  Data_SigmaC14Cal,
  SampleNames,
  Nb_sample,
  PriorAge = rep(c(10, 50), Nb_sample),
  SavePdf = FALSE,
  OutputFileName = c("MCMCplot", "HPD_CalC-14Curve", "summary"),
  OutputFilePath = c(""),
  SaveEstimates = FALSE,
  OutputTableName = c("DATA"),
  OutputTablePath = c(""),
  StratiConstraints = c(),
  sepSC = c(","),
  Model = c("full"),
  CalibrationCurve = c("IntCal20"),
  Iter = 50000,
  t = 5,
  n.chains = 3,
  quiet = FALSE,
  roundingOfValue = 3
)

Arguments

Data_C14Cal

numeric (required): corresponding to C-14 age estimate.

Data_SigmaC14Cal

numeric (required): corresponding to the error of C-14 age estimates.

SampleNames

character (required): names of sample. The length of this vector is equal to Nb_sample.

Nb_sample

integer: number of samples.

PriorAge

numeric (with default): lower and upper bounds for age parameter of each sample in years (not in ka). Note that, length(PriorAge) == 2 * Nb_sample and PriorAge[2i-1,2i] corresponds to the lower and upper bounds of sample whose number ID is equal to i.

SavePdf

logical (with default): if TRUE save graphs in pdf file named OutputFileName in folder OutputFilePath.

OutputFileName

character (with default): name of the pdf file that will be generated by the function if SavePd=TRUE, length(OutputFileName) = =3, see PLOT OUTPUT in Value section for more informations.

OutputFilePath

character (with default): path to the pdf file that will be generated by the function if SavePdf=TRUE. If it is not equal to "", it must be terminated by "/".

SaveEstimates

logical (with default): if TRUE save Bayes' estimates, credible interval at level 68% and 95% and the result of the Gelman and Rubin test of convergence, in a csv table named OutputFileName in folder OutputFilePath.

OutputTableName

logical (with default): name of the table that will be generated by the function if SaveEstimates=TRUE.

OutputTablePath

character (with default): path to the table that will be generated by the function if SaveEstimates=TRUE. If it is not equal to "", it must be terminated by "/".

StratiConstraints

numeric matrix or character(with default): input object for the stratigraphic relation between samples. If there is stratigraphic relation between samples see the details section for instructions regarding how to correctly fill StratiConstraints; the user can refer to a matrix (numeric matrix) or to a csv file (character). If there is no stratigraphic relation default value is suitable.

sepSC

character (with default): if StratiConstraints is character, indicate column separator in StratiConstraints csv file.

Model

character (with default): if "full", error on estimate calibration curve is taken account. If "naive" this error is not taken account in the age estimate.

CalibrationCurve

character (with default): calibration curve chosen. Allowed inputs are

  • "Intcal13" or "Intcal13" for Northern Hemisphere atmospheric radiocarbon calibration curve,

  • "Marine13" or "Marine13" for Marine radiocarbon calibration curve,

  • "SHCal13" or "SHCal20" for Southern Hemisphere atmospheric radiocarbon calibration curve

  • a csv file, with tree columns, the first column is dedicated to "Cal.BP", the second to "XC-14.age", the third to "Error". The decimal of this file must be a dot, and the separator must be a comma.

Iter

integer (with default): number of iterations for the MCMC computation (for more information see rjags::jags.model).

t

integer (with default): 1 every t iterations of the MCMC is considered for sampling the posterior distribution (for more information see rjags::jags.model.

n.chains

integer (with default): number of independent chains for the model (for more information see rjags::jags.model.

quiet

logical (with default): enables/disables rjags messages

roundingOfValue

integer (with default): Integer indicating the number of decimal places to be used, default set to 3.

Value

NUMERICAL OUTPUT

  1. A list containing the following objects:

    • Sampling: that corresponds to a sample of the posterior distributions of the age parameters;

    • Outlier: stating the names of samples that are considered as outliers;

    • Model: stating which model was chosen ("full" or "naive");

    • CalibrationCurve: stating which radiocarbon calibration curve was chosen;

    • PriorAge: stating the priors used for the age parameter;

    • StratiConstraints: stating the stratigraphic relations between samples considered in the model.

  2. The Gelman and Rubin test of convergency: print the result of the Gelman and Rubin test of convergence for the age estimate for each sample. A result close to one is expected.
    In addition, the user must visually assess the convergence of the trajectories by looking at the graph generated by the function (see PLOT OUTPUT for more informations).
    If both convergences (Gelman and Rubin test and plot checking) are satisfactory, the user can consider the estimates as valid. Otherwise, the user may try increasing the number of MCMC iterations (Iter) or being more precise if it is possible on the PriorAge parameter to reach convergence.

  3. Credible intervals and Bayes estimates: prints the Bayes' estimates, the credible intervals at 95% and 68% for the age parameters for each sample.

PLOT OUTPUT

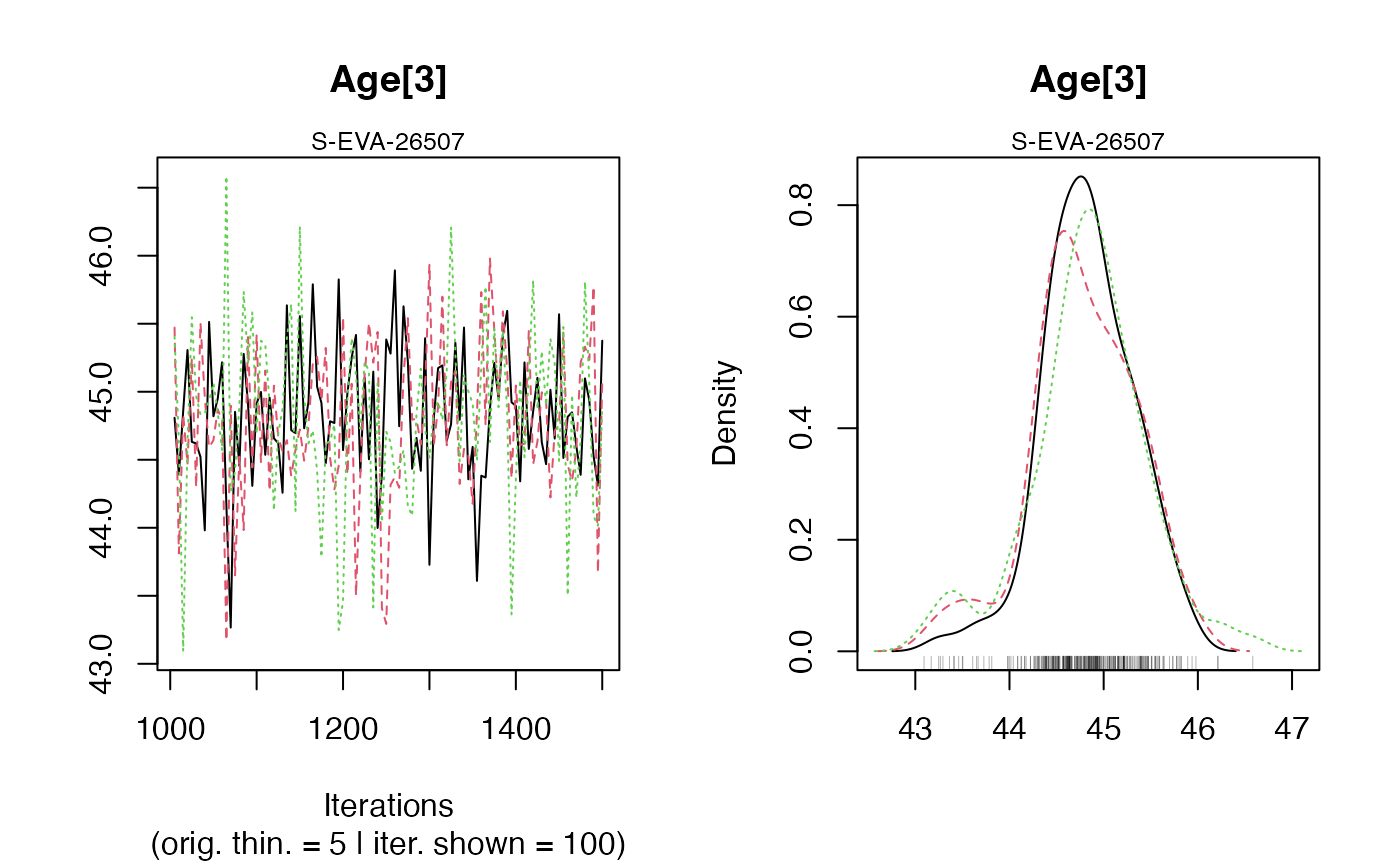
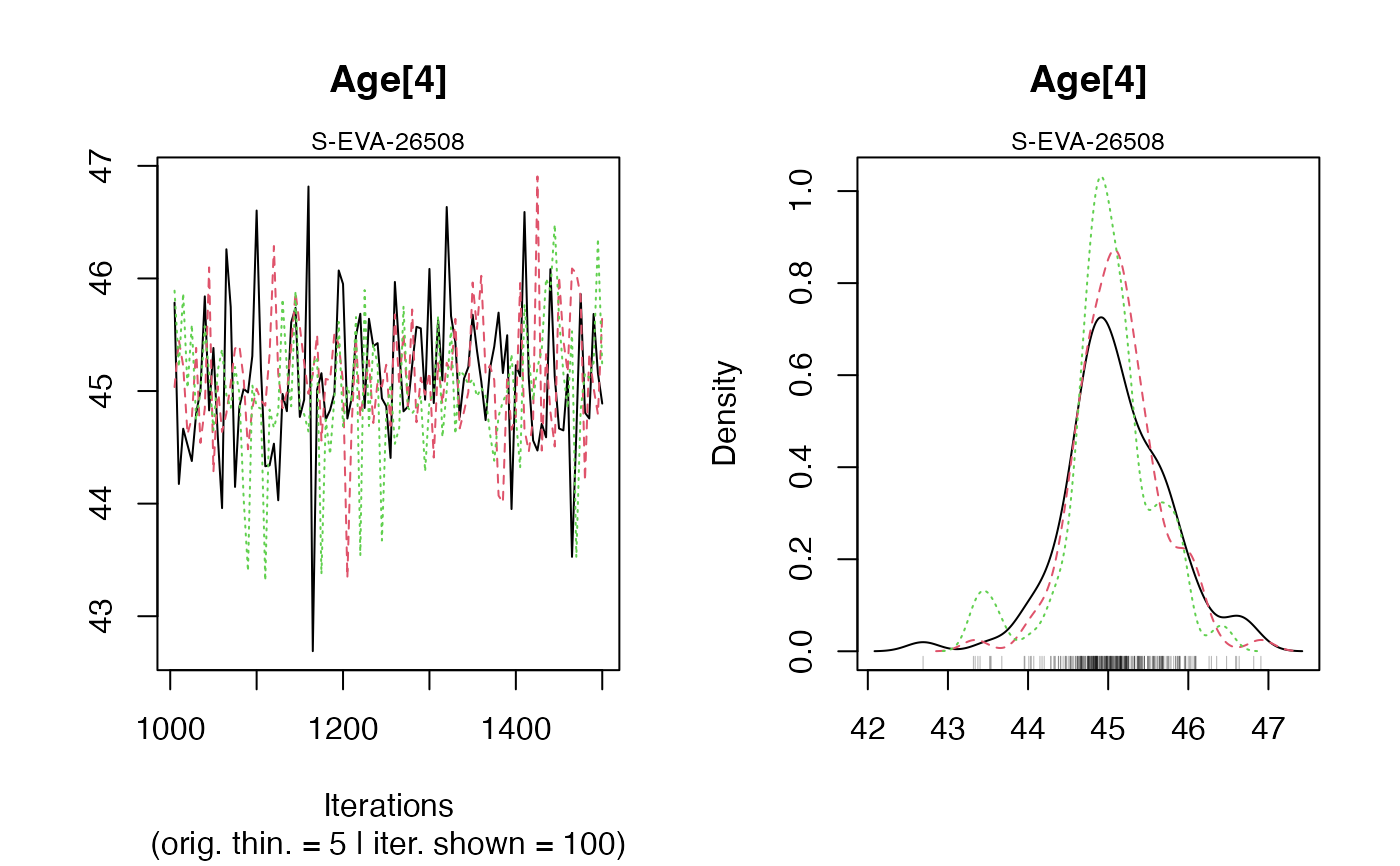
  1. MCMC trajectories: A graph with the MCMC trajectories and posterior distributions of the age parameter is displayed.
    On each line, the plot on the left represents the MCMC trajectories, and the one on the right the posterior distribution of the parameter.

  2. Summary of sample age estimates: plot credible intervals and Bayes' estimate of each sample age on one graph.

To give the results in a publication, we recommend to give the Bayes' estimate of the parameters as well as the credible interval at 95% or 68%.

Details

How to fill StratiConstraints?

If there is stratigraphic relations between samples, C-14 age in Data_C14Cal must be ordered by order of increasing ages.

The user can fill the StratiConstraints matrix as follow.

  1. Size of the matrix: row number of StratiConstraints matrix is equal to Nb_sample+1, and column number is equal to Nb_sample.

  2. First line of the matrix: for all i in {1,...,Nb_Sample}, StratiConstraints[1,i]=1 that means the lower bound of the sample age (given in PriorAge[2i-1]) for the sample whose number ID is equal to i, is taken into account.

  3. Sample relations: for all j in {2,...,Nb_Sample+1} and all i in {j,...,Nb_Sample}, StratiConstraints[j,i]=1 if sample age whose number ID is equal to j-1 is lower than sample age whose number ID is equal to i. Otherwise, StratiConstraints[j,i]=0.

Note that StratiConstraints_{2:Nb_sample+1,1:Nb_sample} is a upper triangular matrix.

The user can also use SCMatrix or SC_Ordered (if all samples are ordered) functions to construct the StratiConstraints matrix.

The user can also refer to a .csv file that contains the relation between samples as defined above. The user must take care about the separator used in the csv file using the argument sepSC.

** More precision on Model **

We propose two models "full" or "naive". If Model = 'full' that means measurement error and error on calibration curve are taken account in the Bayesian model; if Model = "naive" that means only error on measurement are taken account in the mode.

More precisely, the model considered here, as the one developed by Christen, JA (1994), assume multiplicative effect of errors to address the problem of outliers. In addition, to not penalise variables that are not outliers and damage theirs estimation, we introduce a structure of mixture, that means only variable that are considered as outlier have in addition a multiplicative error.

Note

Please note that the initial values for all MCMC are currently all the same for all chains since we rely on the automatic initial value generation of JAGS. This is not optimal and will be changed in future. However, it does not affect the quality of the age estimates if the chains have converged.

How to cite

Christophe, C., Philippe, A., Guérin, G., Kreutzer, S., 2024. AgeC14_Computation(): Bayesian analysis for C-14 age estimations of various samples. In: Christophe, C., Philippe, A., Kreutzer, S., Guérin, G., Baumgarten, F.H., Frerebeau, N., 2024. BayLum: Chronological Bayesian Models Integrating Optically Stimulated. R package version 0.3.2. https://CRAN.r-project.org/package=BayLum

References

Christen, JA (1994). Summarizing a set of radiocarbon determinations: a robust approach. Applied Statistics, 489-503.

Reimer PJ, Bard E, Bayliss A, Beck JW, Blackwell PC, Bronl Ramsey C, Buck CE, Cheng H, Edwards RL, Friedrich M, Grootes PM, Guilderson TP, Haflidason H, Hajdas I, Hatte C, Heaton TJ, Hoffmann DL, Hogg AG, Hughen KA, Kaiser KF, Kromer B, Manning SW, Niu M, Reimer RW, Richards DA, Scott EM, Southon JR, Staff RA, Turney CSM, van der Plicht J. 2013. IntCal13 ans Marine13 radiocarbon age calibration curves 0-50000 years cal BP. Radiocarbon 55(4)=1869-1887.

Hogg AG, Hua Q, Blackwell PG, Niu M, Buck CE, Guilderson TP, Heaton TJ, Palmer JG, Reimer PJ, Reimer RW, Turney CSM, Zimmerman SRH. 2013. SHCal13 Southern Hemisphere calibration, 0-50000 years cal. BP Radiocarbon 55(4):1889-1903

See also

rjags, plot_MCMC, SCMatrix, plot_Ages

Author

Claire Christophe, Anne Philippe, Guillaume Guérin, Sebastian Kreutzer

Examples

## Load data
data(DATA_C14,envir = environment())
C14Cal <- DATA_C14$C14[,1]
SigmaC14Cal <- DATA_C14$C14[,2]
Names <- DATA_C14$Names
nb_sample <- length(Names)

## Age computation of samples without stratigraphic relations
Age <- AgeC14_Computation(
 Data_C14Cal = C14Cal,
 Data_SigmaC14Cal = SigmaC14Cal,
 SampleNames = Names,
 Nb_sample = nb_sample,
 PriorAge = rep(c(20,60),nb_sample),
 Iter = 500,
 quiet = TRUE,
 roundingOfValue = 3)
#> Warning: [plot_MCMC()] 'n.iter' out of range, reset to number of observations




#> 
#> 
#> >> MCMC Convergence of Age parameters <<
#> ----------------------------------------------
#> Sample name   Bayes estimate   Uppers credible interval
#> A_S-EVA-26510 	 1.012 		 1.014 
#> A_S-EVA-26506 	 1.019 		 1.05 
#> A_S-EVA-26507 	 1.008 		 1.012 
#> A_S-EVA-26508 	 1.009 		 1.029 
#> 
#> 
#> ---------------------------------------------------------------------------------------------------
#>  *** WARNING: The following information are only valid if the MCMC chains have converged  ***
#> ---------------------------------------------------------------------------------------------------
#> 
#> 
#> 
#> >> Bayes estimates of Age for each sample and credible interval <<
#> ------------------------------------------------------
#> Sample name 	 Bayes estimate  Credible interval: 
#> A_S-EVA-26510 	 41.9619462839152 
#> 						 lower bound 	 upper bound
#> 				 at level 95% 	 41.494 		 42.361 
#> 				 at level 68% 	 41.819 		 42.249 
#> ------------------------------------------------------
#> Sample name 	 Bayes estimate  Credible interval: 
#> A_S-EVA-26506 	 45.717723231144 
#> 						 lower bound 	 upper bound
#> 				 at level 95% 	 45.155 		 46.287 
#> 				 at level 68% 	 45.522 		 46.018 
#> ------------------------------------------------------
#> Sample name 	 Bayes estimate  Credible interval: 
#> A_S-EVA-26507 	 44.8147702224378 
#> 						 lower bound 	 upper bound
#> 				 at level 95% 	 43.5 		 45.826 
#> 				 at level 68% 	 44.308 		 45.257 
#> ------------------------------------------------------
#> Sample name 	 Bayes estimate  Credible interval: 
#> A_S-EVA-26508 	 45.0752297665528 
#> 						 lower bound 	 upper bound
#> 				 at level 95% 	 43.952 		 46.354 
#> 				 at level 68% 	 44.618 		 45.576 
#> 
#> ------------------------------------------------------