Skip to contents

Dose Rate Estimation

Source: R/AllGenerics.R, R/dose_fit.R, R/dose_predict.R
doserate.Rd

  • dose_fit() builds a calibration curve for gamma dose rate estimation.

  • dose_predict() predicts in situ gamma dose rate.

Usage

dose_fit(object, background, doses, ...)

dose_predict(object, spectrum, ...)

# S4 method for class 'GammaSpectra,GammaSpectrumOrNumeric,matrix'
dose_fit(
  object,
  background,
  doses,
  range_Ni,
  range_NiEi,
  details = list(authors = "", date = Sys.time())
)

# S4 method for class 'GammaSpectra,GammaSpectrumOrNumeric,data.frame'
dose_fit(
  object,
  background,
  doses,
  range_Ni,
  range_NiEi,
  details = list(authors = "", date = Sys.time())
)

# S4 method for class 'CalibrationCurve,missing'
dose_predict(
  object,
  sigma = 1,
  epsilon = 0.015,
  water_content = NULL,
  use_MC = FALSE
)

# S4 method for class 'CalibrationCurve,GammaSpectrum'
dose_predict(
  object,
  spectrum,
  sigma = 1,
  epsilon = 0.015,
  water_content = NULL,
  use_MC = FALSE
)

# S4 method for class 'CalibrationCurve,GammaSpectra'
dose_predict(
  object,
  spectrum,
  sigma = 1,
  epsilon = 0.015,
  water_content = NULL,
  use_MC = FALSE
)

Arguments

object

A GammaSpectra or CalibrationCurve object.

background

A GammaSpectrum object or a length-two numeric vector giving the background noise integration value and error, respectively. If no background subtraction is wanted, you can set background = c(0,0,)

doses

A matrix or data.frame object with gamma dose values and uncertainties. The row names must match the names of the spectrum.

...

Currently not used.

spectrum

An optional GammaSpectrum or GammaSpectra object in which to look for variables with which to predict. If omitted, the fitted values are used.

range_Ni, range_NiEi

A length-two numeric vector giving the energy range to integrate within (in keV).

details

A list of length-one vector specifying additional informations about the instrument for which the curve is built.

sigma

A numeric value giving the confidence level of which the error from the slope is considered in the final uncertainty calculation

epsilon

A numeric value giving an extra relative error term, introduced by the calibration of the energy scale of the spectrum, e.g., 0.015 for an additional 1.5% error

water_content

numeric or matrix gravimetric field water content to correct the gamma-dose rate to using the correction factor by Aitken (1985) to obtain the dry gamma-dose rate. Example: c(0.05,0.0001) for water content of 5% +/- 0.01 %. The default is NULL (nothing is corrected). The correction only works on the final dose rate. For more information see details.

use_MC

A logical parameter, enabling/disabling Monte Carlo simulations for estimating the dose rate uncertainty

Value

  • dose_fit() returns a CalibrationCurve object.

  • dose_predict() returns a data.frame with the following columns:

    name

    (character) the name of the spectra.

    signal_Ni

    (numeric) the integrated signal value (according to the value of threshold; see signal_integrate()) for energy = FALSE

    signal_err_Ni

    (numeric) the integrated signal error value (according to the value of threshold; see signal_integrate()) for energy = FALSE.

    dose_Ni

    (numeric) the predicted gamma dose rate for energy = FALSE.

    dose_err_Ni

    (numeric) the predicted gamma dose rate error for energy = FALSE.

    signal_Ni

    (numeric) the integrated signal value (according to the value of threshold; see signal_integrate()).

    signal_err_NiEi

    (numeric) the integrated signal error value (according to the value of threshold; see signal_integrate()) for energy = TRUE.

    dose_NiEi

    (numeric) the predicted gamma dose rate for energy = TRUE.

    dose_err_NiEi

    (numeric) the predicted gamma dose rate error for energy = TRUE.

    dose_final

    (numeric) the predicted final gamma dose rate as the mean of dose_Ni and dose_NiEi

    dose_err_final

    (numeric) the predicted final gamma dose rate error as \(SE(\dot{D}_{\gamma}) = \sqrt{(\frac{SE(\dot{D}_{\gamma\mathrm{Ni}})}{\dot{D}_{\gamma\mathrm{Ni}}})^2 + (\frac{SE(\dot{D}_{\gamma\mathrm{NiEi}})}{\dot{D}_{\gamma\mathrm{NiEi}}})^2}\)

Details

To estimate the gamma dose rate, one of the calibration curves distributed with this package can be used. These built-in curves are in use in several luminescence dating laboratories and can be used to replicate published results. As these curves are instrument specific, the user may have to build its own curve.

The construction of a calibration curve requires a set of reference spectra for which the gamma dose rate is known and a background noise measurement. First, each reference spectrum is integrated over a given interval, then normalized to active time and corrected for background noise. The dose rate is finally modelled by the integrated signal value used as a linear predictor (York et al., 2004).

Note

See vignette(doserate) for a reproducible example.

Uncertainty calculation of the gamma-dose rate

The analytical uncertainties of the final gamma-dose rate (\(SE(\dot{D}_{\gamma})\)) are calculated as follows:

$$ \sigma_{\dot{D_\gamma}} = \sqrt((\frac{m_{\delta}s}{m})^2 + (\frac{s_{\delta}}{s})^2 + \epsilon^2) $$

with \(m\) and \(m_{\delta}\) being the slope of the fit an its uncertainty, \(\sigma\) the error scaler for the slope uncertainty, \(s\) and \(s_{\delta}\) the integrated signal and its uncertainty, and \(\epsilon\) an additional relative uncertainty term that can be set by the user using the argument epsilon.

If the parameter use_MC is set to TRUE, the a Monte Carlo sampling approach is chosen to approximate the uncertainties on the dose rate:

$$ \sigma_{\dot{D_\gamma}} := \sqrt((\frac{SD(\mathcal{N}(\mu_{slope}, \sigma_{slope}) \times \mathcal{N}(\mu_{signal}, \sigma_{signal}) + \mathcal{N}(\mu_{intercept}, \sigma_{intercept})) * \rho}{\dot{D_\gamma}})^2 + \epsilon^2) * \dot{D_\gamma} $$

\(\ rho\) is the parameter sigma provided with the function call, \(SD\) equals the the call to sd(), i.e. the calculation of the standard deviation. To achieve a good Gaussian normal approximation with sample 1+e06 times (the values is fixed).

Water content correction

If gamma-dose rates are measured in the field, they are measured at "as-is" conditions. In dating studies, however, using the dry dose rate is often more desirable to model the long-term effect of different assumptions for the water content. If the parameter water_content, either as numeric vector or as matrix with the number of rows equal to the number of processed spectra, if different values are desired, the final gamma-dose rate is corrected for the water content provided. Final uncertainties are obtained using the square root of the summed squared relative uncertainties of the dose rate and the water content.

A word of caution: When estimating the water content in the laboratory, the water analytical uncertainty is usually minimal, and it does not make sense to correct with a relative water content of, e.g., c(0.02,0.02) (2% +/- 2%) because this massively inflates the final dose rate error.

References

Aitken, M.J. (1985). Thermoluminescence dating. London: Academic Press.

Mercier, N. & Falguères, C. (2007). Field Gamma Dose-Rate Measurement with a NaI(Tl) Detector: Re-Evaluation of the "Threshold" Technique. Ancient TL, 25(1), p. 1-4.

York, D., Evensen, N. M., Martínez, M. L. & De Basabe Delgado, J. (2004). Unified Equations for the Slope, Intercept, and Standard Errors of the Best Straight Line. American Journal of Physics, 72(3), p. 367-75. doi:10.1119/1.1632486 .

See also

signal_integrate()

Author

N. Frerebeau

Examples

## Import CNF files
## Spectra
spc_dir <- system.file("extdata/BDX_LaBr_1/calibration", package = "gamma")
spc <- read(spc_dir)

## Background
bkg_dir <- system.file("extdata/BDX_LaBr_1/background", package = "gamma")
bkg <- read(bkg_dir)

## Get dose rate values
data("clermont")
(doses <- clermont[, c("gamma_dose", "gamma_error")])
#>        gamma_dose gamma_error
#> BRIQUE  1986.4620   35.619679
#> C341     849.9668   21.317615
#> C347    1423.8589   25.249756
#> GOU     1575.2249   17.433789
#> LAS     1083.6737    9.570593
#> LMP      641.9004   17.560649
#> MAZ     1141.4033   11.665045
#> MPX      964.0196   13.274167
#> PEP     2538.2217  112.169131

## Build the calibration curve
calib_curve <- dose_fit(spc, bkg, doses,
                        range_Ni = c(300, 2800),
                        range_NiEi = c(165, 2800))
#> Warning: All spectra without energy calibration. You can proceed but it is not recommended!

## Plot the curve
plot(calib_curve, threshold = "Ni")


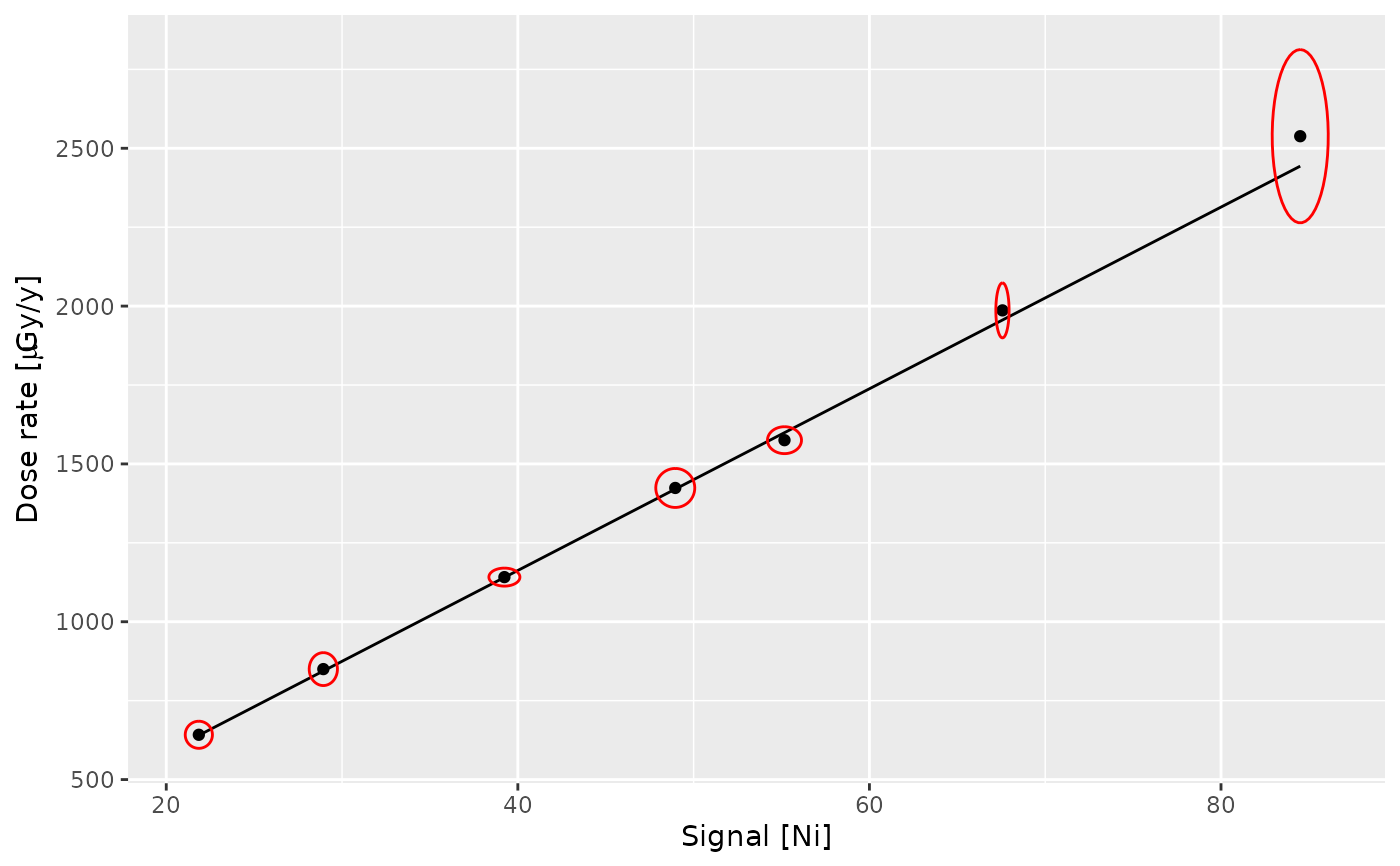## Estimate gamma dose rates
dose_predict(calib_curve, spc)
#>     name signal_Ni signal_err_Ni   dose_Ni dose_err_Ni signal_NiEi
#> 1 BRIQUE  67.56799     0.1088753 1953.8126    51.04781    64025.06
#> 2   C341  28.93445     0.2321450  844.2413    23.03416    27700.15
#> 3   C347  48.95519     0.3204599 1419.2451    38.15865    46110.29
#> 4    GOU  55.16875     0.2796524 1597.7011    42.44396    52563.01
#> 5    LMP  21.85261     0.2236734  640.8480    17.95295    20987.25
#> 6    MAZ  39.23547     0.2551738 1140.0909    30.64143    37607.71
#> 7    PEP  84.50625     0.4606470 2440.2863    65.01209    80089.25
#>   signal_err_NiEi dose_NiEi dose_err_NiEi dose_final dose_err_final
#> 1        3.453506 1946.9570      49.02259  1950.3848       70.77024
#> 2        7.462936  843.0632      21.22872   843.6523       31.32285
#> 3       10.141403 1402.5373      35.31587  1410.8912       51.97214
#> 4        8.865474 1598.6316      40.25289  1598.1664       58.49693
#> 5        7.236250  639.0619      16.09246   639.9549       24.10606
#> 6        8.156462 1144.1487      28.80962  1142.1198       42.06299
#> 7       14.465409 2435.1387      61.31599  2437.7125       89.36030